Lightning Strike

[Kinerd]

Short Version

Process rate: 1.45% ± 0.30%
Average damage: 610

.

Very Long Version

Process Rate
I recorded 14520 swings against the training dummy with my exploiter. I did so with a single Lit II khopesh and no sources of double-strike. Of these, 706 were misses and 200 were lightning strikes. The process rate is therefore:
200 / (14520 - 706) = 1.45%

To determine standard deviation, I calculate the variance as:
(14520 - 706) * (1.45%) * (1 - 1.45%)

Taking the square root to obtain standard deviation and multiplying by 3, I obtained the 0.30% figure. This means that there is a ~99.7% chance that the actual process rate is somewhere between 1.75% and 1.15%.

Damage Dice
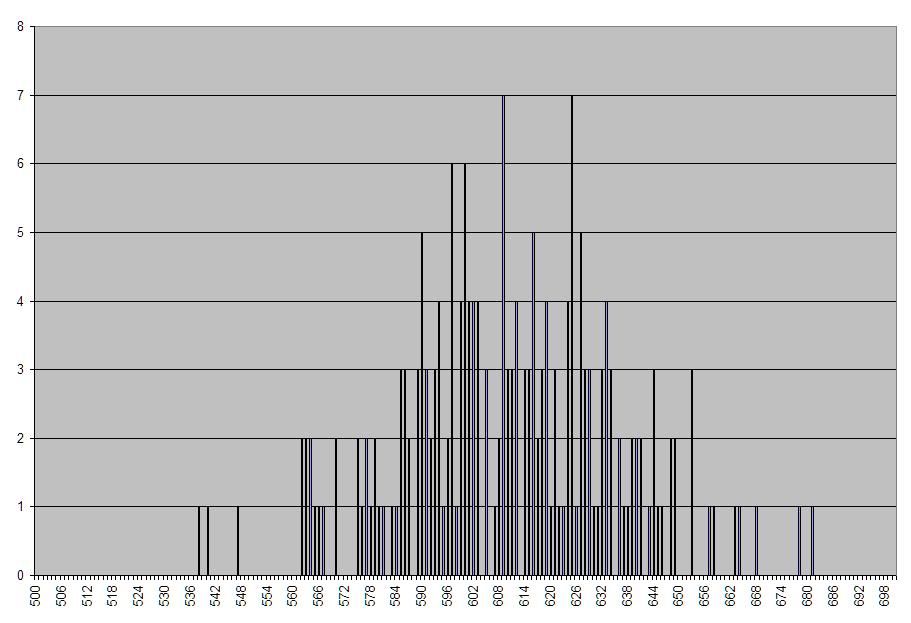
I also recorded the damages done on each lightning strike, taking into account the helpless state when appropriate. The raw data is as follows:

As we would expect with such a low data to bin ratio, the graph is very ugly. This does not prevent us from calculating a standard deviation, however, which I found to be 25. What this means is that ~68% of the values fall within 25 bins of 610, or from 635 to 585. By extrapolation, this also means that we expect ~99.7% of all future values to fall within 75 bins of 610, or from 685 to 535, very close to the commonly held belief that lightning strike ranges from ~500 to ~700.

We can reasonably expect that the underlying distribution for lightning strike damage is dice-based, which means that it is a normal distribution, which in turn means that it is totally described by the standard deviation and average value: the average tells us where it is, the standard deviation tells us how broad it is. We can also obtain the variance directly from any hypothetical dice distribution with the following equation:
variance of xdn = x * (n^2 - 1) / 12

And since we have a value for standard deviation, we can work backwards by setting n to certain common values and obtaining values for x:

d6	214.2857143
d8	119.047619
d10	75.75757576
d12	52.44755245
d20	18.79699248

We can now apply some general observations about DDO:
1. There are no fractional dice; that is, there could be 214d6 or 215d6, but not 214.285d6.
2. Generally round numbers are used, so 120 seems more likely than 119, 50 more likely than 52, and so on.
3. Generally there are only positive flat damage modifiers; we see lots of d6 + 2 types, but not d8 - 4 or d10 - 1.

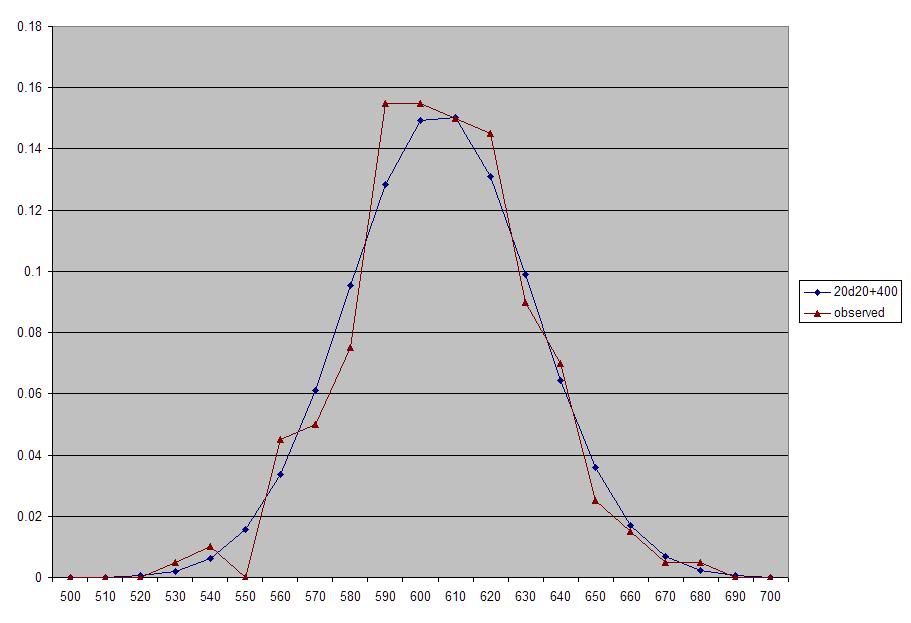
For instance, if we do 215d6, the average value of the dice is 215 * 3.5 = 752.5, which means lightning strike would have to be 215d6 - 240 to fit both the observed average and standard deviation. By point 3, this seems unlikely, and it also raises the possibility (however remote) of negative damage. To my mind, the most likely candidate is 20d20 + 400. Here is a graph of the distribution against the current data, consolidated into bins of ten, so "500" represents all data from 500-509, and so on:

While the model is labeled 20d20 + 400, it's important to stress that the distributions are effectively interchangeable. The points where they differ are only at the edges: 20d20 has a total range of 381, while 215d6 has a total range of 1076. By construction, however, both distributions have the same generally expected distribution, which is to say standard deviation. As such, it's only reasoning that can feasibly rule them in or out. Take 20d20: the only way to see the very edge of the range is to roll a 1 on every d20, or (1/20)^20, which works out to 1 in 10^26, or 1 in 100 trillion trillion. It's simply not practical to wait for such edge cases to present themselves, and 20d20 is the best case. The worst case (215d6) is 1 in 10^167.

.

I will continue to collect data, but this seemed like a good point to get some results out there.

[krackythehoodedone]

So about 1 proc in 75 swings then ish ish.

MM i like the pretty pictures, nice job

And the Strike Graphic is awesome

For your next exploration into the seedy world of probability

Please tell me what proc/guard dishes out the most Whoopass

In mathematical terms obviously

[somenewnoob]

Can some people on this mans server give him some plat to fund a study of other proc rates so we can finally find out how much all this stuff procs!

+1, nice work.

[Aliss7]

I recorded 14520 swings

How did you automate the recording and collection of this data? I know people have asked that the combat logs be recorded somewhere, but AFAIK that hasn't been provided?

Edit Add: BTW, you win DDO Nerd Award of the Day. And I mean this in the most sincere way possible.

[Vanshilar]

To add to the data, I've got 51 procs out of 3335 non-miss (i.e. excluding rolls of 1) hits, which is mean 1.53% and 95% confidence interval of 1.17% to 2.00%. The average damage was 614, with a standard deviation of 30. This would work out to something like 30d20 + 300.

It's interesting to see that we get different standard deviations, since that "should" be more or less consistent with different sample sizes; obviously though the smaller the sample size, the larger the variation in standard deviations across different tests, and 51 hits wasn't particularly large. At any rate though, the average damage is what people generally care about, and it seems like our averages are pretty close. For what it's worth, this works out to around 8.5-9 damage per hit attempt (i.e. a TWF typically gets 1.8 hit attempts per swing, 1 main hit attempt and 0.8 offhand hit attempts on average), depending on whose figures you're using.

[Chette]

Very nice, I've been trying to find reliable data on lightning strike, as well as some of the other effects available on alchemical weapons. This will be very helpful!

[DragonTroy]

woah, this is really freaking impressive, thanks for the valuable information

1 in 75 hits? man now i really want my monk to have some lit2 wraps

[Stermlin]

[Kinerd]

How did you automate the recording and collection of this data? I know people have asked that the combat logs be recorded somewhere, but AFAIK that hasn't been provided?

All manual, I'm afraid, though there is something to be said for a notebook page fiiiiilled with tally marks.

For your next exploration into the seedy world of probability

Please tell me what proc/guard dishes out the most Whoopass

In mathematical terms obviously

When I'm satisfied with the lit2, the next thing I intend to look at is the Radiant Blast effect on the epic Mabar handwraps. I don't really have any characters that use guards, I'm afraid, someone else will have to check those out.

I appreciate everyone's comments. Thanks.

[Stillwaters]

Im a math ****** - so forgive me

1 proc in 75 attacks (average)
610 lightning damage(Average)

So LitII adds 8.13 damage per attack?

[Kinerd]

Got it in one, Stillwaters.

Strictly speaking, there is some statistical uncertainty in both the rate and damage, so the experimentally determined value for Lightning Strike is 8.13 ± something, but your arithmetic is correct.

[Mr_Tank]

+1

[pal_sch]

Easyplot? Bonus points for not using Excel.

Really nice method using the standard deviation like that, but I can't quite believe that anyone would manually record that many attacks. So glad you did given the last time I remember this being attempted was based on people trying to remember their best and worst strikes.

[sho-gun]

+1. Awesome stuff.

And lols to the head splody comic

[Eladrin]

A virtual +1 to you. (My +1's don't do anything. Very sad. So you get information instead.)

Lightning Strike on weapons is 1.5% application probability, and is indeed 20d20+400 electrical damage.

[grodon9999]

A virtual +1 to you. (My +1's don't do anything. Very sad. So you get information instead.)

Lightning Strike on weapons is 1.5% application probability, and is indeed 20d20+400 electrical damage.

Sigh . . . so our "12 points a swing" assumption was wrong? Good to finally have accurate info.

[sephiroth1084]

All manual, I'm afraid, though there is something to be said for a notebook page fiiiiilled with tally marks.When I'm satisfied with the lit2, the next thing I intend to look at is the Radiant Blast effect on the epic Mabar handwraps. I don't really have any characters that use guards, I'm afraid, someone else will have to check those out.

I appreciate everyone's comments. Thanks.

I'm constantly in awe of both your math/statistics skills and your incredible patience, Kinerd! Bravo!

I'd actually really like to see a write-up for Disintegration, which leads me to...

A virtual +1 to you. (My +1's don't do anything. Very sad. So you get information instead.)

Lightning Strike on weapons is 1.5% application probability, and is indeed 20d20+400 electrical damage.

Any chance you could give us the numbers for this stuff outright? I know that it's probably fun for you to see players working it out for themselves (finally nailed it down after almost 4 years), and probably holds some enjoyment for those who do the working out, like Kinerd and Vanshilar, but it would be nice to actually know how all this stuff works without waiting 4 years for definitive information.

[LeLoric]

Sigh . . . so our "12 points a swing" assumption was wrong? Good to finally have accurate info.

yep it's 9.15, significant enough to drop many situations where litII was considered better to where it isn't.

[ainmosni]

Any chance you could give us the numbers for this stuff outright?

heh, it appears we have to figure it out ourselves, that's a lot of tedious work, and a 'that's correct' from a dev is a reward i'd be more than happy with.


well, that and some FRDS. i like them. they're like cookies, but inedible and can be turned into armor.

+1 to you, sir.

[danotmano1998]

Wow..

To be honest, I've never seen statistical math before.
I'm still not entirely sure exactly what all the jargon means exactly, but hey, you nailed it!

Confirmed by a dev and a virtual +1!

So, I'll give you a +1 for him.