Vanshilar's Attack Speed Index and Formulae

[Vanshilar]

This thread is for some testing results and analysis on the attack swing animation speeds for different styles of fighting.

On terminology: In Update 5, two weapon fighting (TWF) offhand attacks have become probabilistic, rather than in a set sequence. Furthermore, the main hand can have a chance to strike twice, or "doublestrike". Because of this, there may be some confusion when I talk about "attack speeds", since it may refer to multiple things. For this thread, I will generally be talking about the character's swing animations per minute, or how often they make a new swing animation (while standing still), not the proc rate of different attacks (main hand, offhand, glancing blows, doublestrike) per minute. "Alacrity" also means swing animations per minute, by the way. I will sometimes shorten "swing animations per minute" to "SPM".

Summary of results:
* Alacrity bonuses add together when they stack
* Fast THF (greataxe, quarterstaff) swings per minute (BAB 20) is 86.50 * (100% + 1.0327 * sum of each boost%)
* Slow THF (greatsword) swings per minute (BAB 20) is 86.63 * (100% + 0.9615 * sum of each boost%)
* Fast THF twitch swings per minute (BAB 20) is 99.49 * (100% + 1.2763 * sum of each boost%)
* Slow THF twitch swings per minute (BAB 20) is 102.22 * (100% + 1.1302 * sum of each boost%)
* TWF swings per minute (BAB 20) is 86.66 * (100% + 1.1965 * sum of each boost%) (note TWF gets about 20% more than THF from each percentage of boost)
* Unarmed (monk) swings per minute (BAB 20) is 93.23 * (100% + 1.2939 * sum of each boost%)

Tested alacrity boosts (alacrity modifiers):
* Jorgundal's collar gives a 10% boost (enhancement)
* Madstone boots gives a 10% boost (enhancement)
* Haste (spell) gives a 15% boost (enhancement)
* Haste boost (skill) 1, 2, 3, and 4 give 15%, 20%, 25%, 30% boosts
* Rogue Acrobat I gives 10% boost to quarterstaff
* Rogue Acrobat II gives 5% boost to quarterstaff (total 15% since would also have Acrobat I)
* Monk Wind Stance I gives 7.5% boost (enhancement) to unarmed (doublestrike chance not tested, other weapons not tested)

Note that enhancement bonuses do not stack with each other; only the highest one applies.

To plug into the formula, find the sum total of all applicable boosts, then plug that amount (as a percentage) into the above "sum of each boost%". Note that this is just the swing speed; doublestrike, offhand, and glancing blow proc rates effectively are multiplied by this.

You can also use the chart below:

BAB 20 swing animations per minute
Boost%	fTwitch	sTwitch	Unarmed	TWF	fastTHF	slowTHF
0%	99.5	102.2	93.2	86.7	86.5	86.6
5%	105.8	108.0	99.3	91.8	91.0	90.8
10%	112.2	113.8	105.3	97.0	95.4	95.0
15%	118.5	119.5	111.3	102.2	99.9	99.1
20%	124.9	125.3	117.4	107.4	104.4	103.3
25%	131.2	131.1	123.4	112.6	108.8	107.5
30%	137.6	136.9	129.4	117.8	113.3	111.6
35%	143.9	142.7	135.5	123.0	117.8	115.8
40%	150.3	148.4	141.5	128.1	122.2	119.9
45%	156.6	154.2	147.5	133.3	126.7	124.1
50%	163.0	160.0	153.5	138.5	131.2	128.3
55%	169.3	165.8	159.6	143.7	135.6	132.4
60%	175.7	171.5	165.6	148.9	140.1	136.6

Note that although the chart lists up to 60%, currently, for all styles, only up to 45% is possible, with the exception of fastTHF where rogue acrobat 2 with quarterstaff can get up to 60% (note that I have not tested quarterstaff twitching).




Testing procedure:

The testing was done in a tavern so that I can regen my clickies while testing. Due to processing limitations (i.e. my laptop sucks), I only video recorded a 320 x 240 part of the screen, at 10 frames per second, however at high quality. The last three lines of the combat log were recorded in the video, to see when boosts started and wore off. On later videos, I had the bright idea of also recording part of my hotbars and the frame rate, to provide visual confirmation as to whether or not the settings I used were correct (i.e. in a video that says the jorgundal's collar was used, whether or not it was actually used), and also to see if there was (processing) lag during the test. The tests were done in the past few days (9/17/2010-9/18/2010), so this is post-Update 6 and pre-Update 7.

Because I did my testing with a rogue multiclass (BAB 16), the start of each test was to cast divine power. I have tested that there is an attack speed difference with using or not using divine power (around 1%), so it seems to work in giving me a full BAB 20 attack speed.

The next part was to cast the haste spell if testing with it, then to activate either haste boost (if I'm testing it) or sprint boost (if I'm not testing haste boost), so that either way, there is a consistent 20-second timer. As soon as I hit a boost, I press the attack key, so any delay between activation and when the character starts swinging is due to the activation timer (the character does not have quickdraw) and not my laziness, so that I get the most time possible under boosted conditions.

During analysis, I visually compared the frames from where I first started swinging to the last identical swing before the boost ended (i.e. if I used the first 2nd swing animation to start my comparison, then I also used the last 2nd swing animation before the boost ended to compare). I then noted which frames they were at. Then I went through and counted how many swings were between the two. Because different swings animations have different speeds, these were always done in multiples of an attack sequence, i.e. 4 swings. Thus the number of attacks were 4, 8, 12, 16, etc. in each test. I then divide by the time difference between the start and end, and multipled by 60 to get a figure for swings per minute (SPM). An example of this is below:



Because I can visually compare the frames at the beginning and end of each test, I can ensure that they were "synced up" (i.e. at the same part of the swing animation or very close to it) to reduce the measurement error. On average, the total time from beginning to end of each test was around 17.6 seconds. Because the video was 10 frames per second, and I am choosing the end frame that matches the start frame the best (or vice versa), the error is at most 1 frame, or 0.1 seconds, or 0.57% of the total time. In other words, the attack speed measurements have a measurement error of 0.57%. Of course, there are other sources of error (such as lag), but the error due to the measurement process itself should only be this much.

The videos were recorded under a wide variety of conditions. The different settings included:

Enhancement bonus to alacrity: 0% (none), 10% (jorgundal's collar), or 15% (haste clickie)
Action boost bonus to alacrity: 0% (none), 15% (haste boost 1), 20% (haste boost 2), 25% (haste boost 3), or 30% (haste boost 4)
Competence bonus to TWF alacrity: 0% (none), or 10% (tempest)

The setups included using dwarven axes (daxe) for TWF and a greataxe (gaxe) for two-handed fighting (THF). I also did some testing with khopesh (khop) and greatsword (gsword) but haven't gone through them yet. There are a variety of other setups that I'll post about when I get to them.

I will upload the videos that I used to analyze onto Youtube so that anyone who wants to can go through them and analyze them. There's over 100 videos that I've made so far, so it may take a while for me to get them up.


Testing analysis:

THF:
The testing was done with a greataxe (gaxe). I did record the testing using a greatsword (gsword) as well, but haven't gone through them yet. The testing results were as follows:

total frames from start to end:
enh_bonus	0%	15%	20%	25%	30%
none (0%)	167	167	184	176	169
collar (10%)	175	176	170	183	176
haste (15%)	168	169	184	177	171

attack swing rounds (multiply by 4 for number of swings):
enh_bonus	0%	15%	20%	25%	30%
none (0%)	6	7	8	8	8
collar (10%)	7	8	8	9	9
haste (15%)	7	8	9	9	9

swings per minute:
enh_bonus	0%	15%	20%	25%	30%
none (0%)	86.2	100.6	104.3	109.1	113.6
collar (10%)	96.0	109.1	112.9	118.0	122.7
haste (15%)	100.0	113.6	117.4	122.0	126.3

Let me know if this ends up not being formatted correctly.

In looking through this data, it should be apparent that the swing speed with multiple alacrity bonuses look pretty similar (or even identical) to the swing speed of just one alacrity bonus that's the sum of them. What I mean is that for example, the swing speed of the collar (10%) with 15% haste boost is 109.1 SPM, which is also the swing speed of just a single 25% haste boost. If they weren't identical, they were at most around 0.7 SPM off, which is just a 1-frame difference (limits of the measurement error).

So with this in mind, I can organize the data by moving the collar (10%) and haste (15%) rows to the right, in line so that the total sums of the bonuses line up:

boost	0%	10%	15%	20%	25%	30%	35%	40%	45%
none	86.2		100.6	104.3	109.1	113.6			
collar		96.0			109.1	112.9	118.0	122.7	
haste			100.0			113.6	117.4	122.0	126.3
average	86.2	96.0	100.3	104.3	109.1	113.4	117.7	122.4	126.3

The bottom row is the average of those numbers where multiple ones exist.

Now, if you do a regular X-Y scatter plot of this data, you'll see that it ends up being pretty close to a straight line:



However, the base SPM (i.e. without any bonuses) is a little bit low, by around 1 SPM or so. It's possible that this is just the limits of the measurement error (although it's above the measurement error) or something; after all, there was only one test of this, so there may have been other issues such as lag. At any rate, if we ignore that data point for now, the linear plot becomes somewhat cleaner:



If you look at the y = mx + b trendline equation, it should be a little bit striking how close the m and the b are. In fact, it turns out that the observed SPM (except without any boosts) will be very close to the following formula:

THF swings per minute = 87.2 * (100% + sum of each boost%)

with the caveat that in the absence of any boosts, THF swing speed is around 86.2 SPM. The error between this formula and the above experimental results is at most about +-0.30 SPM, or +-0.28% of the values.

Remember that this was tested using a gaxe; I'll update if I find out that gsword SPM measurements are different from this, or, for that matter, if it turns out that different races have different swing speeds (this was tested using a dwarf).

TWF:
In much the same vein, I can do the same for TWF. Testing was done with a daxe and khop, but I haven't analyzed the khop data yet so this data is using the daxe results. First, the data:

total frames from start to end:
enh_bonus	0%	15%	20%	25%	30%
none (0%)	166	165	178	170	183
collar (10%)	174	170	184	176	169
haste (15%)	188	183	176	187	180

attack swing rounds (multiply by 4 for number of swings):
enh_bonus	0%	15%	20%	25%	30%
none (0%)	6	7	8	8	9
collar (10%)	7	8	9	9	9
haste (15%)	8	9	9	10	10

swings per minute:
enh_bonus	0%	15%	20%	25%	30%
none (0%)	86.7	101.8	107.9	112.9	118.0
collar (10%)	96.6	112.9	117.4	122.7	127.8
haste (15%)	102.1	118.0	122.7	128.3	133.3

There's an interesting quirk to this. Because my testing character also has the tempest prestige enhancement, and the tempest prestige enhancement currently still gives a 10% alacrity bonus, I have an additional source of alacrity boost to test with. Unfortunately I have to wait 3 days to respec to test the "in between" haste boost amounts, but here are the values for the tempest without using boosts and using the 30% boost:

total frames from start to end:
enh_bonus	0%	30%
none (0%)	173	187
collar (10%)	179	173
haste (15%)	170	184

attack swing rounds (multiply by 4 for number of swings):
enh_bonus	0%	30%
none (0%)	7	10
collar (10%)	8	10
haste (15%)	8	11

swings per minute:
enh_bonus	0%	30%
none (0%)	97.1	128.3
collar (10%)	107.3	138.7
haste (15%)	112.9	143.5

In the same way as with THF, these can be shifted to the right to line up with the sum of the boosts:

boost	0%	10%	15%	20%	25%	30%	35%	40%	45%	50%	55%
none	86.7		101.8	107.9	112.9	118.0					
collar		96.6			112.9	117.4	122.7	127.8			
haste			102.1			118.0	122.7	128.3	133.3		
t_none		97.1						128.3			
t_coll				107.3						138.7	
t_haste					112.9						143.5
average	86.7	96.8	102.0	107.6	112.9	117.8	122.7	128.2	133.3	138.7	143.5

where the "t_" indicates the tempest values.

Just like with THF, the swing speeds can be plotted by the amount of boosts:



The results are pretty close to a straight line, even when there are no boosts involved. However, there's somewhat of a problem: the m and b do not match up. In fact, it turns out that m (which is the benefit per percent of alacrity boost) is 1.1965x that of b (which is the base swings speed). In other words, unlike THF, TWF actually gets a 6% swing speed increase for every 5% alacrity boost. For example, my tempest rogue, fully buffed up, gets a 55% boost (tempest 10% + haste 15% + haste boost 30%), but this turns out to provide an actual 66% increase in the number of attacks per minute, whereas a THF that got a 55% boost would have a 55% increase in the number of attacks per minute. Anyway, the formula for TWF would be:

TWF swings per minute = 86.6 * (100% + 1.2*sum of each boost%)

The error between this formula and the above experimental results are all within about +- 0.36 SPM, or +-0.32% of the values.


How this compares with previous work done on attack speed:

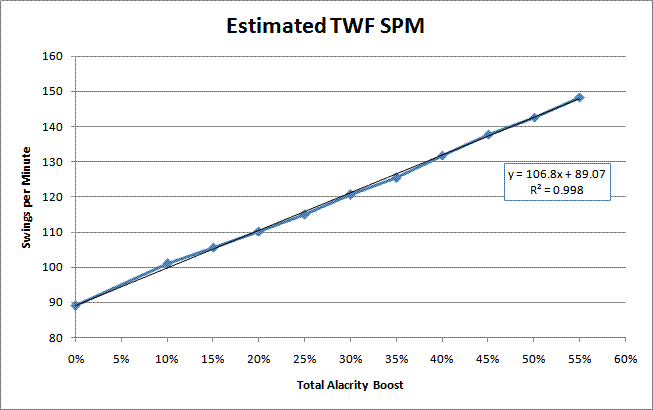
There has already been some studies done of attack speeds; for example, cforce's thread is here and Monkey_Archer's thread is here, and I'm sure there are others that escape my mind at the moment (feel free to let me know if there were others on attack speeds that I missed). However, those studies, and the DPS calcs derived from them, were done using duration (how long each swing lasts) as the base variable, where I use swing rate (how many swings per unit time) as the base variable. The previous work was also based on some developer comments as to how stacking works, namely, that the duration is decreased by the given bonus percentage and that different bonuses will stack multiplicatively. Unfortunately, fitting that model necessitated the use of "overhead" values and other fudge terms in the formula to make it fit the experimental data. Although the system may indeed use such values to ensure that the swing durations are appropriate, we as players are more concerned with the actual effect of those duration changes. Here, it would seem like the effect of the changes is that the swings per minute -- and thus the DPS increases linearly, according to the sum total of all the boosts. Indeed, if cforce's attack speed estimator were used and the results recorded, the estimated values would be:

boost	0%	10%	15%	20%	25%	30%	35%	40%	45%	50%	55%
none	89.0		105.5	110.6	116.2	122.4					
collar		100.9			114.5	119.8	125.7	132.2			
haste			105.5			119.5	125.0	131.1	137.8		
t_none		100.9						132.2			
t_coll				109.6						142.6	
t_haste					114.5						148.4
estim	89.0	100.9	105.5	110.1	115.0	120.6	125.4	131.9	137.8	142.6	148.4

which (looking at the trendline formula) is very close to my formula except that the base SPM is 89.1 rather than my 86.6. The difference may be due to performance differences between my POS laptop and cforce's top-notch system, server-side usage, recent updates, or a combination of the above and other factors. Otherwise, though, the resulting data is pretty similar. Of course, conceptually, it is much easier to think of a 10% alacrity bonus as "10% more DPS" rather than to muck around with overhead and such, which I think is the advantage of my formula.

I will post some additional results in other attack styles as I get around to analyzing them.

[Vanshilar]

This post will just be a library of links to Youtube videos of the tests as I upload them, with the tested SPM where available. The naming convention for the Youtube videos are: "attack speed" (enhancement bonus: "none", "collar", or "haste") (haste boost amount: "0", "15", "20", "25", "30") (weapon such as "daxe" or "gsword") (special notes such as "tempest")

THF using greataxe (fast THF):

enh_bonus	0%	15%	20%	25%	30%
none (0%)	86.2	100.6	104.3	109.1	113.6
collar (10%)	96.0	109.1	112.9	118.0	122.7
haste (15%)	100.0	113.6	117.4	122.0	126.3

THF using greatsword (slow THF):

enh_bonus	0%	15%	20%	25%	30%
none (0%)	86.5	N/A	103.7	N/A	111.6
collar (10%)	94.9	N/A	N/A	N/A	N/A
haste (15%)	N/A	N/A	115.5	N/A	124.1

TWF using dwarven axe:

enh_bonus	0%	15%	20%	25%	30%
none (0%)	86.7	101.8	107.9	112.9	118.0
collar (10%)	96.6	112.9	117.4	122.7	127.8
haste (15%)	102.1	118.0	122.7	128.3	133.3

TWF using khopesh:

enh_bonus	0%	15%	20%	25%	30%
none (0%)	N/A	N/A	N/A	N/A	N/A
collar (10%)	N/A	N/A	N/A	N/A	N/A
haste (15%)	N/A	N/A	N/A	N/A	N/A

TWF using dwarven axe, with tempest:

enh_bonus	0%	15%	20%	25%	30%
none (0%)	97.1	N/A	N/A	N/A	128.3
collar (10%)	107.3	N/A	N/A	N/A	138.7
haste (15%)	112.9	N/A	N/A	N/A	143.5

TWF using khopesh, with tempest:

enh_bonus	0%	15%	20%	25%	30%
none (0%)	N/A	N/A	N/A	N/A	N/A
collar (10%)	N/A	N/A	N/A	N/A	N/A
haste (15%)	N/A	N/A	N/A	N/A	N/A

Unarmed (monk):

enh_bonus	0%	15%	30%
none (0%)	92.8	N/A	N/A
wind (7.5%)	102.4	120.3	N/A
collar (10%)	105.3	123.8	N/A
haste (15%)	111.3	129.7	147.1

THF twitch using greataxe (fast twitch):

enh_bonus	0%	15%	20%	25%	30%
none (0%)	99.4	118.0	124.9	131.9	137.9
collar (10%)	112.1	131.1	137.1	143.2	150.8
haste (15%)	119.3	137.7	143.2	150.9	156.5

THF twitch using greatsword (slow twitch):

enh_bonus	0%	15%	20%	25%	30%
none (0%)	102.4	119.7	125.3	131.5	137.1
collar (10%)	113.3	131.1	137.3	142.0	149.1
haste (15%)	119.6	136.5	142.4	148.3	154.2

[Consumer]

Nice, Quickdraw or not?

[k1ngp1n]

Nicely done, +1.

[AltheaSteelrain]

reading comprehension check: rolling die

correct me if I'm wrong, but did I see both THF and TWF melee's having equal swing speeds? O.o

I thought TWF is faster...

[mystafyi]

you are an analytical genius.


I also noticed that twf and thf spm were about the same? doesnt make sence to mah inferior mind. perhaps you could post some conclusions you have come to?

[Vanshilar]

Some things:

* My character does not have quickdraw. However, it's not particularly important as to whether or not he did, since I took the difference between the frame at which he started attacking (roughly) and the last identical attack before the boost ran out (roughly) for the timing, rather than just counting up how many attacks while the boost is active. This increases the measurement's accuracy and precision.

* You can see that the base swings per minute for THF and TWF are similar. However, TWF benefits more from each percent of alacrity boosts (haste spell, etc.) -- they get 6% more DPS for every 5% of boost, while THF only gets 5%. Since generally you will have some amount of boost, this means that in general TWF will indeed swing faster. Just that unbuffed, etc., they have very close swing speeds.

* I've started uploading Youtube videos, so you can click on the links in the library to see the videos for yourself (or if you want to do some analysis on them).

* By recasting attack speeds in this way, hopefully an intuitive understanding and analysis of DPS is greatly simplified. For example, based on this, it is fairly easy to see that the doublestrike mechanic was actually a boon for THF fighters and paladins, relative to the other classes. For a THF fighter, the capstone, whose alacrity bonus stacked additively pre-Update 5, previously meant an increase in attack speed from 150% of base to 160% of base (with +20% from madstone and +30% from haste boost), or a DPS increase of 6.7%. However, now, the capstone, by giving a 10% doublestrike chance, which stacks multiplicatively with attack (swing) speed, means an increase from 145% of base (with +15% from haste spell and +30% from haste boost) to 145%*1.1 = 159.5% of base. So you can see that the doublestrike mechanic more or less canceled out the nerf of madstone, while all other classes basically had to absorb the madstone nerf. So it becomes much easier to discuss DPS in this way rather than having to go through all the offsets and such, and hopefully discussion can be much more concrete rather than having to rely on a black box.

[KKDragonLord]

I have to say that these seem to be the most reliable source of data regarding attack speeds i have seen i a very long time.

Are you planning on calculating Twitch speeds for us THFs to consider?

[zealous]

Unfortunately, fitting that model necessitated the use of "overhead" values and other fudge terms in the formula to make it fit the experimental data.

Actually, except for modeling multiplicative duration decrease instead of additive attack rate increase, it's exactly the same as your models.

Summary of results:
* Alacrity bonuses add together
* THF swings per minute is 87.2 * (100% + sum of each boost%), or 86.2 if no bonuses exist Fudge factor
* TWF swings per minute is 86.6 * (100% + 1.2*sum of each boost%) (note TWF get 20% more than THF from each percentage of boost) different overhead

Or to put it into other words:
Fudge factor: Base attack rate doesn't fit the model
Overhead: Alacricity effects different fighting styles differently, most noticeable for ranged, discrepancy between non-twitch 2h, unarmed and armed.

Indeed, if cforce's attack speed estimator were used and the results recorded, the estimated values would be:

You are not using that model fitted to your data compared with your measurements!

One really interesting thing is what you get when you use only parts of the data to fit the model, and then predict the measurements not used to fit the model.

And another how many measurements are of single/double/tripple alacricity effects =)


Still, you are doing it wrong even if it's more practical!

[Vanshilar]

Actually, except for modeling multiplicative duration decrease instead of additive attack rate increase, it's exactly the same as your models.

The problem is that those are fundamental differences in how the models are constructed. That's like saying an airplane is basically a bicycle except for the wings.

Or to put it into other words:
Fudge factor: Base attack rate doesn't fit the model
Overhead: Alacricity effects different fighting styles differently, most noticeable for ranged, discrepancy between non-twitch 2h, unarmed and armed.

Uh you should look at what fudge factor really means. In this case saying that the swings per minute for THF follows a different formula when there are no haste modifiers is an example of a special case, in the same way that 0! (factorial) is defined to be 1.

The original introduction of overhead, by assuming that part of the swing animation is affected by alacrity modifiers and part of the swing is not (the latter part being the overhead), is fundamentally different than the concept that different styles get different bonuses from haste. If the data is that different styles do get different bonuses, of course any attack speed model will have that as part of the model. Trying to justify calling it overhead when it serves a different purpose (the modifier I use is a coefficient on the haste bonus, the m in y = mx + b, while overhead is a constant, or the b in y = mx + b) is just an exercise in semantics. In this case you reframed "overhead" to mean that "alacrity effects different fighting styles differently" when the original use of the term is the portion that is not affected by alacrity, conflating the difference between what a variable is and what it's used for.

You are not using that model fitted to your data compared with your measurements!

It's not necessarily for me to fit that model to my data. The point was to show that the model will actually generate a (roughly) straight line if looked at from the perspective of swings per minute.

If you consider the original basic model, that the duration is (1 - modifier1) * (1 - modifier2) * (1 - modifier3) etc. and that the swings per minute is the reciprocal of this, then modifiers will actually stack multiplicatively. However, the actual data is that they stack additively, meaning that the swings per minute is based on (1 + modifier1 + modifier2 + modifier3) etc. These two are fundamentally different, which is why it was necessary to introduce overhead and such. And so my point was that the original model, even though the fundamental structure was incompatible, with the help of such fudge factors was able to match the actual data, i.e. an additive model.

I actually have a sneaking suspicion that if I go through cforce's original data and tried to fit an additive model to it, it would actually work out fairly smoothly. Haven't tried it though, so can't say for sure.

One really interesting thing is what you get when you use only parts of the data to fit the model, and then predict the measurements not used to fit the model.

No idea what you're saying here.

And another how many measurements are of single/double/tripple alacricity effects =)

Well, you can see that in my data. In fact that's one of the charts for each style is, lining up a 10% tempest alacrity plus 15% haste action boost with a single 25% haste action boost, etc. Again no idea what you're saying here.

Still, you are doing it wrong even if it's more practical!

When fitting a model to experimental data, any reasonable measure of its veracity is how well it fits the data. So I don't see how you're saying that it's wrong when it fits the data to a error margin significantly less than 1% (basically, to the limits of the experimental error). Please name another model that can fit the actual data more accurately. Is it because you expect a multiplicative model, even though the data fits an additive model a lot more clearly than a multiplicative one? In that case, where's the evidence to justify that a multiplicative model is more accurate?

A secondary measure of a model is its usefulness, i.e. how easily it can be understood and used. In that measure I suppose we're in agreement, but that's also somewhat of a secondary issue.

[zealous]

The problem is that those are fundamental differences in how the models are constructed. That's like saying an airplane is basically a bicycle except for the wings.

Only if the airplane flies, if it never does they behave functionally the same.

Would you expect to get significantly different results for either a multiplicative duration or a additive attack rate model fitted to your data?

Uh you should look at what fudge factor really means. In this case saying that the swings per minute for THF follows a different formula when there are no haste modifiers is an example of a special case, in the same way that 0! (factorial) is defined to be 1.

The way I see it, cforce states that the "special case" of no modifiers doesn't follow the model, you state that the "special case" of no modifiers doesn't follow the model.
Maybe doing a separate regression disregarding the no modifiers points is significantly better than adding a fudge factor, might be that they're functionally more or less the same.

What's pretty undisputable is that you probably don't care if you have slight errors while you might care about the practical use of having one general model as opposed to multiple specific ones. That's my guess why he put it there at least, get a workable general model an all. =)

The original introduction of overhead, by assuming that part of the swing animation is affected by alacrity modifiers and part of the swing is not (the latter part being the overhead), is fundamentally different than the concept that different styles get different bonuses from haste. If the data is that different styles do get different bonuses, of course any attack speed model will have that as part of the model. Trying to justify calling it overhead when it serves a different purpose (the modifier I use is a coefficient on the haste bonus, the m in y = mx + b, while overhead is a constant, or the b in y = mx + b) is just an exercise in semantics. In this case you reframed "overhead" to mean that "alacrity effects different fighting styles differently" when the original use of the term is the portion that is not affected by alacrity, conflating the difference between what a variable is and what it's used for.

Not really. If we assume that weapon attack speeds are indeed normalized to swing at the same speed, I.e. a*x+b is constant at leas for the no modifier case. If one weapon style has a lower b, how can we keep it at the same normalized attack speed? Indeed, by increasing a.

And this is exactly how it works in cforces model, both a and b are different between 2h and 2wf, same as in your models.

Let me rephrase that one more time: The important thing is not the overhead variable, it's the total duration subtracted by the overhead.

The model could as easily have been written with constants for a, i.e. duration affected by haste, and have overhead calculated using the total duration.

It's not necessarily for me to fit that model to my data. The point was to show that the model will actually generate a (roughly) straight line if looked at from the perspective of swings per minute.

Well allow me to do that for you then =)

multiplicative duration modifiers for th

1.00 0.8500 0.80 0.7500 0.700
0.90 0.7650 0.72 0.6750 0.630
0.85 0.7225 0.68 0.6375 0.595

Your measured durations for 2h

0.6960557 0.5964215 0.5752637 0.5499542 0.5281690
0.6250000 0.5499542 0.5314438 0.5084746 0.4889976
0.6000000 0.5281690 0.5110733 0.4918033 0.4750594

fit with all points gives a a of 0.53175 and a b of 0.15069, F-statistic looks good, R-squared looks good, "somewhat" high residuals for first/last point going by your standards.

Fit without the no modifer point we get a of 0.498012 and a b of 0.174479, F-statistic looks good, R-squared looks good, residuals looks good.

Wow, the model fits pretty much perfectly, then this must truly be the real deal!???

If you consider the original basic model, that the duration is (1 - modifier1) * (1 - modifier2) * (1 - modifier3) etc. and that the swings per minute is the reciprocal of this, then modifiers will actually stack multiplicatively. However, the actual data is that they stack additively, meaning that the swings per minute is based on (1 + modifier1 + modifier2 + modifier3) etc. These two are fundamentally different, which is why it was necessary to introduce overhead and such. And so my point was that the original model, even though the fundamental structure was incompatible, with the help of such fudge factors was able to match the actual data, i.e. an additive model.

The actual data is that we can't determine how it really works since both models fit well enough.
See above re overhead.
See above re fudge factor.

I actually have a sneaking suspicion that if I go through cforce's original data and tried to fit an additive model to it, it would actually work out fairly smoothly. Haven't tried it though, so can't say for sure.

You have the data, you have the model, should be fairly straight forward to determine what amount of boostage would be needed to determine a significant difference between the alternate models, yah?

No idea what you're saying here.

Overfitting? cross validation?

Well, you can see that in my data. In fact that's one of the charts for each style is, lining up a 10% tempest alacrity plus 15% haste action boost with a single 25% haste action boost, etc. Again no idea what you're saying here.

Let's say we have 60% of samples from cases where there aren't any stacking of effects, 30% of samples from cases where there is stacking of two effects and 10% of samples from cases where there is stacking of two effects. Would a accurate model be more likely to fit cases where there is no stacking better or cases where there is stacking?

When fitting a model to experimental data, any reasonable measure of its veracity is how well it fits the data. So I don't see how you're saying that it's wrong when it fits the data to a error margin significantly less than 1% (basically, to the limits of the experimental error). Please name another model that can fit the actual data more accurately. Is it because you expect a multiplicative model, even though the data fits an additive model a lot more clearly than a multiplicative one? In that case, where's the evidence to justify that a multiplicative model is more accurate?

That would depend on what you plan to use the model for. Since using it to predict already known and accurately measured data would be somewhat unnecessary, maybe how well it can predict and model previously unknown stuff would be better?
Also, see above.

A secondary measure of a model is its usefulness, i.e. how easily it can be understood and used. In that measure I suppose we're in agreement, but that's also somewhat of a secondary issue.

I'd say it being reasonable and generally applicable are two quite important points too.

[Vanshilar]

Well I wasn't going to explicitly get into which formula is correct, but if you really want to...

Would you expect to get significantly different results for either a multiplicative duration or a additive attack rate model fitted to your data?

The multiplicative duration model is:

duration = A * (1 - a) * (1 - b) * (1 - c) * ... + B

with A and B being constants, and a, b, c, etc. are the alacrity modifiers (so haste boost 1 would be 0.15, jorgundal's collar would be 0.1, etc.). Converted into swings per unit time (i.e. per minute), it then becomes:

swings per minute = 1 / [ A * (1 - a) * (1 - b) * (1 - c) * ... + B ]

However, for my additive model, the swings per minute is:

swings per minute = C * [1 + D*(a + b + c + ...) ]

These two formulae are mutually incompatible, that is, given A and B constants for the first equation, it is generally impossible to find C and D for the second equation that would match up with the first equation for arbitrary values of a, b, c. In other words, it is generally impossible to find A, B, C, and D such that the following holds:

1 / [ A * (1 - a) * (1 - b) * (1 - c) * ... + B ] = C * [1 + D*(a + b + c + ...) ]

for arbitrary a, b, c, etc. Or at least, I wasn't able to. If you find a solution, let me know.

So this means that there is one that is correct and one that is not (or possibly, that both are not). In other words, there is a fundamental difference in the structure of the model, which is what I said before. What it remains to do then is to see which one can actually match the data.

In the multiplicative duration model, using A = 0.498012 and B = 0.174479, this is what I get for the duration for two-handed (let me know if you got something different):

0.67249	0.59779	0.57289	0.54799	0.52309
0.62269	0.55546	0.53305	0.51064	0.48823
0.59779	0.53429	0.51313	0.49196	0.47080

By contrast, this is what I get by using my model above (i.e. C = 87.2 and D = 1), converted into duration (in seconds):

0.68807	0.59832	0.57339	0.55046	0.52929
0.62552	0.55046	0.52929	0.50968	0.49148
0.59832	0.52929	0.50968	0.49148	0.47453

If we now take the percentage error, that is:

(model's predicted value - data's value) / data's value

then for the multiplicative model above, it becomes:

-3.385%	0.229%	-0.413%	-0.358%	-0.962%
-0.370%	1.001%	0.302%	0.425%	-0.158%
-0.368%	1.159%	0.402%	0.032%	-0.897%

while for the linear additive model, it is:

-1.147%	0.319%	-0.325%	0.092%	0.212%
0.083%	0.092%	-0.406%	0.238%	0.508%
-0.279%	0.212%	-0.272%	-0.066%	-0.111%

Now both models don't do well when there's no boosts at all (the upper left cell). However, as explained in my post, due to the testing methodology, the resolution of the measurement was 1 video frame (0.1 sec), and so that's the measurement error. The average testing length was 17.6 seconds, so this works out to a percentage error of 0.57%. Thus an error below this may simply be due to limits of the testing method, but an error above this is not explained by the measurement methodology and is due to modeling error, lag, computer processing load, etc. The multiplicative duration model has no less than 4 out of 14 (non-unboosted) values that are above this measurement error, while all the predicted values (except the unboosted case, which was disregarded) for the additive model are within this error.

"Now wait" you say, "maybe there was something wrong, or your computer is really crappy and unsteady when you made those videos, and all that bad stuff...the difference wasn't that much beyond the measurement error" and you'd have a point. The problem is that there were only two kinds of boosts used for THF, an enhancement bonus (from haste spell or the collar) and the bonus from the haste action boost. However, the difference between an additive model and a multiplicative model is going to be at the edges of the situations, in other words, a linear function and a nonlinear function will be relatively similar in normal circumstances (where you made the fit), and differ as you move away from them. This is roughly the justification for using small-angle approximations and more generally, Taylor series expansion, that nonlinear and linear (or, polynomial) functions will be closely approximate within a given (small) range.

The key then is to add more boosts (or have very few boosts), or more generally, to have a wide range of boosts, to get to the edges of the situations. Fortunately, because of the tempest bug, this can be done. If you go back to my post, you'll see that for THF, the tested range was from 0% to 45% of the base attack speed, whereas for TWF, the range was 0% to 55% -- or actually, 0% to 66% if you include that TWF gets more benefit from alacrity bonuses. Unfortunately, I haven't gotten around to filling out the rest of the tempest chart yet. However, I can insert the tempest data in with the rest of the TWF data, in swings per minute:

enh_bon	0%	temp10%	15%	20%	25%	30%	t+30%
none	86.7	97.1	101.8	107.9	112.9	118.0	128.3
collar	96.6	107.3	112.9	117.4	122.7	127.8	138.7
haste	102.1	112.9	118.0	122.7	128.3	133.3	143.5

where "temp10%" refers to the tempest alacrity 10% bonus but no haste boosts, the percentages refer to the amount of haste boost, and "t+30%" refers to tempest alacrity along with 30% haste boost. If you prefer the data in terms of duration:

enh_bon	0%	temp10%	15%	20%	25%	30%	t+30%
none	0.69167	0.61786	0.58929	0.55625	0.53125	0.50833	0.46750
collar	0.62143	0.55938	0.53125	0.51111	0.48889	0.46944	0.43250
haste	0.58750	0.53125	0.50833	0.48889	0.46750	0.45000	0.41818

How this data was arrived at is explained in my first post, I just combined the TWF and TWF tempest data sets together.

To fit this data using a multiplicative duration model, the best I could come up with was:

A = 0.546725
B = 0.120909

Let me know if you can find better values for the constants A and B. I ignored the duration for the unboosted case in my best-fit. The data ended up being (in duration):

enh_bon    0%    temp10%    15%    20%    25%    30%    t+30%
none	0.66763	0.61296	0.58563	0.55829	0.53095	0.50362	0.46535
collar	0.61296	0.56376	0.53915	0.51455	0.48995	0.46535	0.43090
haste	0.58563	0.53915	0.51592	0.49268	0.46945	0.44621	0.41368

Using the above TWF formula (C = 86.6 and D = 1.2), I get:

enh_bon    0%    temp10%    15%    20%    25%    30%    t+30%
none	0.69284	0.61861	0.58715	0.55874	0.53295	0.50944	0.46814
collar	0.61861	0.55874	0.53295	0.50944	0.48792	0.46814	0.43303
haste	0.58715	0.53295	0.50944	0.48792	0.46814	0.44990	0.41737

If you again take the percentage error, you'll find that for the multiplicative duration model, the percentage error for each scenario is:

enh_bon    0%    temp10%    15%    20%    25%    30%    t+30%
none	-3.475%	-0.792%	-0.621%	0.367%	-0.056%	-0.928%	-0.461%
collar	-1.363%	0.783%	1.488%	0.673%	0.217%	-0.873%	-0.369%
haste	-0.319%	1.488%	1.492%	0.776%	0.416%	-0.842%	-1.076%

For the additive model, it's:

enh_bon    0%    temp10%    15%    20%    25%    30%    t+30%
none	0.170%	0.121%	-0.362%	0.448%	0.321%	0.218%	0.136%
collar	-0.454%	-0.113%	0.321%	-0.327%	-0.199%	-0.279%	0.121%
haste	-0.059%	0.321%	0.218%	-0.199%	0.136%	-0.023%	-0.193%

For the TWF case, you can see that even disregarding the unboosted case (which was not used to find the optimal A and B), there are no less than 13 out of the remaining 20 scenarios in which the discrepancy between the model's predicted value and the data is greater than the measurement error -- some by nearly 1.5%, which would represent a 2.6-frame difference from the actual data (easily observable when the measurement's resolution is 1 frame). By contrast, the linear model matches all observed scenarios within the measurement error -- and as a bonus, predicts the unboosted amount as well.

Furthermore, the errors in the multiplicative model are not random -- they are negative at the low end (little boosts), positive in the middle (medium boosts), and negative again at the high end (lots of boosts), which is exactly what you'd expect if you are trying to fit a nonlinear curve to a linear set of data (consider what happens if you try to fit an exponential curve to some linear data: the errors would be one direction at the ends, and the opposite direction in the middle). As a side note, remember that though I gave the data in terms of durations of a swing, in terms of swings per minute, the additive model is linear with respect to the alacrity modifiers whereas the multiplicative model is basically hyperbolic (nonlinear). I thought maybe there's some kind of test to determine if perhaps the model you're using is fundamentally different than the data, but can't think of it off the top of my head.

Returning to the unboosted attack speed, other than loading up on boosts, the other edge is to not have any boosts. In this case, the linear additive model for TWF fits pretty well with the data even for the unboosted case, while THF was off by -1.147%. However, this was due to disregarding that data point explicitly and treating it as a special case (and not trying to fit it). If I had chosen to include it instead, the formula for THF would have been 86.6215 * (1 + 1.0307*sum of alacrity modifiers), and the resulting percentage error (in terms of duration) would have been:

-0.487%	0.586%	-0.170%	0.145%	0.171%
0.471%	0.145%	-0.446%	0.110%	0.299%
-0.014%	0.171%	-0.399%	-0.273%	-0.393%

Note that now, all errors are actually within the measurement error. For the 0.586% case (which is slightly above the given average measurement error of 0.57%), that test was actually out of 167 frames, so its actual measurement error was 1/167 = 0.599%. So had I chosen to, both of my formulas for THF and TWF could have included the unboosted attack speed and would still have remained within the bounds of the measurement error.

By contrast, if the multiplicative model had tried to take into account the unboosted attack speed without the use of the "fudge factor" 0.95, then fully 8 out of the 15 THF scenarios would have ended up outside of the measurement error, indicating modeling problems. And for TWF, it would've made it 15 out of 21 TWF scenarios that would exceed the measurement error, with multiple scenarios being around 1.8% off from observed values. So treating unboosted THF attack speed was a luxury for my model -- it was not necessary within the bounds of measurement error, but I preferred a better match to the rest of the data -- whereas it was absolutely necessary for the multiplicative model to treat unboosted THF and TWF as separate cases, since it was an "edge" case. This is why the original formulation had that "fudge factor" of 0.95 thrown into the mix for when alacrity bonuses are involved -- it was to change the value of A for the unboosted case but to use a different A in all the other cases (i.e. when there are alacrity bonuses) in order to fit the data, whereas in my linear additive model no changes were needed -- I just preferred to lay it out separately.

Last thing I wanted to point out about the THF unboosted scenario, is that a percentage error of -1.147% was significant enough for me to treat it as a special case, while for TWF, the percentage error for the multiplicative model exceeds this amount 4 times -- 5 if you count the unboosted case. And for THF, the multiplicative model doesn't exceed this (except in the unboosted case of course) but approaches it (>+-0.9% error) 4 times, yet is considered "fits pretty much perfectly" with the data. That this difference was big enough for me to make it into a special case while it was small enough to be considered "fits pretty much perfectly" for the multiplicative model speaks volumes about how accurately each model can match the experimental results.

So the multiplicative model actually is demonstrably off from observed results, beyond what can be accounted for by experimental measurement error, with as much as a quarter-second difference during the time of a haste boost (around 17.6 seconds was the average testing length), while a linear model fits all the current data to within 0.1 seconds (the limits of the testing). You can draw your own conclusions from there.

You are welcome to see if you can find A and B for the multiplicative model that fit the data better. It's always possible that Excel found the wrong local optimum when I ran the solver routine.

F-statistic looks good, R-squared looks good, residuals looks good.

Wow, the model fits pretty much perfectly, then this must truly be the real deal!???

There's no need to appeal to more complicated statistical tests such as the F-test in this case, since interpreting them (i.e. what values are good or bad) depends on the situation. For example, the R-squared may have looked pretty good, but the model's error is demonstrably higher than what is accounted for by measurement error, indicating problems with the modeling -- which the R-squared value won't tell you. After all, you probably got something like R^2 = 0.998 for the multiplicative model (at least I did in the first post) which usually indicates a pretty good fit; however, it's still not good enough in this case due to the precision of the measurement. And if you did the same analysis with the additive model, I'd bet you'll find that by those tests it'd look even better.

I'd say it being reasonable and generally applicable are two quite important points too.

I personally think that the additive model is a lot easier to work with than trying to fit in a hyperbolic formula (which is what the multiplicative model end up being). It's much more intuitive to think a 15% haste spell and a 20% haste boost means 15%+20%=35% more DPS rather than the amount of time needed to figure out how the multiplicative model works.

[MrCow]

I decided to revisit some of my attack speed numbers being it appears folks are looking at attack speeds again. While I'm not going to the extent of uploading footage, I can verify that Vanshilar's theory on haste being additive is correct (at least, in some sense it is). DDO does translate 10% bonus to attack speed + 30% bonus to attack speed = 40% bonus to attack speed (and likewise, 5% bonus - 10% penalty = 5% penalty).

However, because of the standardization that occurred updates ago on several melee styles of attack there isn't always a pretty formula to follow. Depending on your Base Attack Bonus, Style of Attack, and/or haste bonus amount determines how long a full animation cycle of attacks takes you via a lookup table. Due to this, some attack styles appear mostly linear (Two-Weapon Fighting with weaponry, One-Handed Weapon Fighting, Fast Two-Handed Weapon Fighting) while others are somewhat exponential (Slow Two-Handed Weapon Fighting Hasted, Unarmed Monk) as they were hand-picked total animation times that fit certain patterns.

For the following table please keep the following in mind:

• 1HF - Stands for "One Handed Fighting", with or without a shield
• TWF - Stands for "Two Weapon Fighting"
• THF - Stands for "Two Handed Fighting"
• Fast THF - Refers to using a Maul or Greataxe
• Slow THF - Refers to using a Greatclub, Falchion, Greatsword, or Quarterstaff
• Unarmed - Refers to a monk's unarmed attacks
• BAB - Stands for "Base Attack Bonus"
• The only Base Attack Bonus points that increase your non-temporal afflicted speed (no slows or hastes) are 0, 1, 3, 5, 10, 15, and 20.
• Hasted values have a completely seperate table. Being under the effects of hastes or slows completely voids any values in the Base Attack Bonus table from being used for some attack cases (which means 15% Haste at BAB 3 is the same exact speed as when you are at BAB 20, at least it was circa update 5 for me 1HF and Quarterstaff, but not necessarily for unarmed). Assume the table refers to BAB 20.
• Being it is currently impossible to have a BAB 0 with the monk unarmed attack sequence that is left blank.
• Animation times refer to the amount of time it takes to complete the 4 attack cycle. For attack cycles with less than 4 attacks the time is adjusted to reflect the average time for 4 attacks.
• A table with values for slowed animations is not included as I haven't invested much time into it yet.
• Currently 0% Haste is a theoretical value. However, values like 2.5% Haste do fit as expected in the pattern between 0% Haste and 5% Haste, thus it is included.

Animation Time BAB Table

BAB	TWF/1HF	FastTHF	SlowTHF	Unarmed		
0	3.00	3.00	3.00		
1	2.96	2.96	2.96	2.80	
3	2.93	2.93	2.93	2.75	
5	2.90	2.90	2.90	2.70	
10	2.86	2.86	2.86	2.65	
15	2.82	2.82	2.82	2.60	
20	2.78	2.78	2.78	2.55	

Attacks Per Minute BAB Table

BAB	TWF/1HF	FastTHF	SlowTHF	Unarmed	
0	80.00	80.00	80.00		
1	81.08	81.08	81.08	85.71	
3	81.91	81.91	81.91	87.27	
5	82.76	82.76	82.76	88.89	
10	83.92	83.92	83.92	90.57	
15	85.11	85.11	85.11	92.31	
20	86.33	86.33	86.33	94.12

Animation Time Haste Table

Haste %	TWF/1HF	FastTHF	SlowTHF	Unarmed		
0%	2.74	2.70	2.80	2.50	
5%	2.61	2.60	2.70	2.40	
10%	2.48	2.50	2.60	2.30	
15%	2.35	2.40	2.50	2.20	
20%	2.22	2.30	2.40	2.10	
25%	2.12	2.20	2.30	2.00	
30%	2.03	2.11	2.20	1.90	
35%	1.95	2.03	2.10	1.80	
40%	1.88	1.97	2.00	1.70	
45%	1.80	1.90	1.90	1.60

Attacks Per Minute Haste Table

Haste %	TWF/1HF	FastTHF	SlowTHF	Unarmed		
0%	87.59	88.89	85.71	96.00	
5%	91.95	92.31	88.89	100.00	
10%	96.77	96.00	92.31	104.35	
15%	102.13	100.00	96.00	109.09	
20%	108.11	104.35	100.00	114.29	
25%	113.21	109.09	104.35	120.00	
30%	118.23	113.74	109.09	126.32	
35%	123.08	118.23	114.29	133.33	
40%	127.66	121.83	120.00	141.18	
45%	133.33	126.32	126.32	150.00

[Vanshilar]

Due to this, some attack styles appear mostly linear (Two-Weapon Fighting with weaponry, One-Handed Weapon Fighting, Fast Two-Handed Weapon Fighting) while others are somewhat exponential (Slow Two-Handed Weapon Fighting Hasted, Unarmed Monk) as they were hand-picked total animation times that fit certain patterns.

To nitpick, they're not actually exponential, they're hyperbolic, basically A/(B-x), since the duration decreases linearly. The actual term is convex, although it's also sometimes called "superlinear" which sounds cooler. But those are more obscure terms which is why I said it's nitpicking I'm sure people know what you mean though.

Anyway, I looked at some of my greatsword data, and it seems like greatsword is linear:

Haste%	Data	Convex
0%	86.5	85.71
10%	94.9	92.31
20%	103.7	100
30%	111.6	109.09
35%	115.5	114.29
45%	124.1	126.32

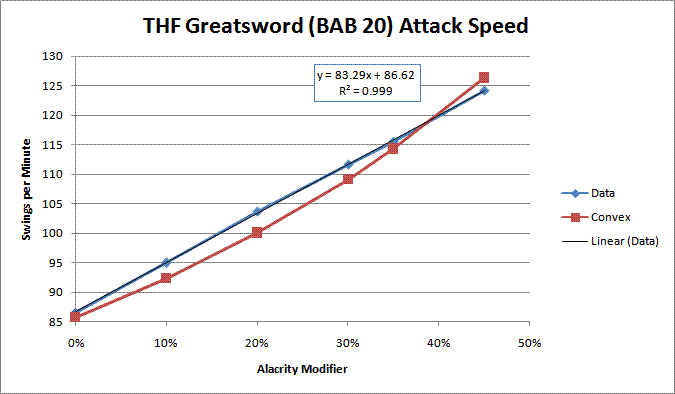
It is however, slightly slower than the greataxe, by about 1.7%, which is statistically significant (since the measurement error is around 0.6%), so there may indeed be different speeds for different weapons. For the quarterstaff, the data matches the THF greataxe data within 1 frame (0.6% percentage error), and so it seems to also be linear, but part of the "fast THF" group. So I think the convex data probably needs to be re-looked at to see if they're really linear or not.

[*]Hasted values have a completely seperate table. Being under the effects of hastes or slows completely voids any values in the Base Attack Bonus table from being used (which means 15% Haste at BAB 3 is the same exact speed as when you are at BAB 20).

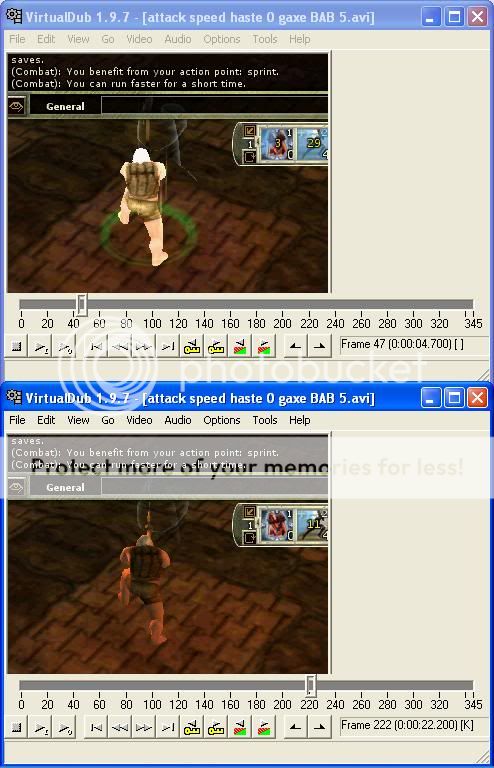
I made a video of a level 6, BAB 5 dwarf swinging a (THF) greataxe, with only the haste spell (15%) as a alacrity modifier:

http://www.youtube.com/watch?v=Tqwz53sS1-I

The result was that it took 222 - 47 = 175 frames (17.5 seconds) to complete 7 rounds (28 swings), or 96 swings per minute, which is less than the value of 100 swings per minute for a BAB 20 THF greataxe. However, BAB 5 does look to be about 95.9% the speed of BAB 20, so it looks like BAB does affect swings per minute even when there are alacrity modifiers.



The annoying thing about studying swing speeds, of course, is that it takes quite a bit of resources (time, setup, etc.) to do it with any depth, and they can easily fit under the "unannounced changes" part of any update, so it's difficult to know what things may have changed after some time.

[Vanshilar]

I haven't played a monk, so I created one on Lamannia to test unarmed attack speeds. The setup was a half-elf 3 monk 1 fighter, the fighter level so that I can have a haste boost. Thus the BAB was +3/+4. I tested three factors:

*with or without haste boost 1
*with or without wind stance activated
*with or without haste spell (from potion)

for a total of 8 tests. The videos are here:

unarmed unbuffed
unarmed boost
unarmed wind
unarmed pot
unarmed boost wind
unarmed boost pot
unarmed wind pot
unarmed boost wind pot

The results were:

# of frames	boost0	boost15
nohaste nowind	188	178
nohaste wind	170	184
haste nowind	178	170
haste wind	178	171

# of rounds	boost0	boost15
nohaste nowind	7	8
nohaste wind	7	9
haste nowind	8	9
haste wind	8	9

swings per min	boost0	boost15
nohaste nowind	89.4	107.9
nohaste wind	98.8	117.4
haste nowind	107.9	127.1
haste wind	107.9	126.3

Again, the video was recorded at 10 frames per second. Each attack round was 4 swing animations. The measurement error is 1 frame, so with an average testing length of 17.7 seconds, the measurement error was around 0.57%, or varied from 0.48 SPM to 0.75 SPM (depending on the test).

A couple of conclusions from this:
* Lesser wind stance provides a 7.5% alacrity bonus which does NOT stack with the 15% from the haste spell.
* A linear fit gives that the formula is:
Unarmed swings per minute (BAB +3/+4) = 89.4 * (100% + 1.39*sum of each boost%)

Note that this is for BAB +3/+4, not capped BAB. If MrCow's BAB numbers are any indication, this implies that the base swings per minute in the formula above would be around 96.4.

The interesting thing is that as you can see, not only is it linear, but every 5% of boost provides almost 7% of actual swings per minute (and thus DPS) increase for unarmed (with at least 1 level of monk). Compare this with 6% of actual swings per minute for TWF, and 5% of actual swings per minute for THF. This means that monks do very well when there are lots of alacrity modifiers, since they will benefit more than other classes from such modifiers. However, it looks like wind stance, or at least the lesser one, does not stack with the haste spell.

[karl_k0ch]

Kudos for this awesome thread.

Do you know of or plan to do a similar attack rate analysis for the ranged attacks, especially with and without manyshot?

And sorry that I can't +1 you right now, but I have to spread some rep before doing it again.

[Zansobar]

I would love to see a comparison done for ranged attacked, repeaters AND bows. If what you say here is true then repeaters actually do more attacks per minute than melee, which would help to narrow the dps gap.

[karl_k0ch]

I would love to see a comparison done for ranged attacked, repeaters AND bows. If what you say here is true then repeaters actually do more attacks per minute than melee, which would help to narrow the dps gap.

There is an ongoing Ranged Speed test (how long does it take to fire 100 Arrows) in the Ranger forums: http://forums.ddo.com/showthread.php?t=276658

Unfortunately, I don't know of any Repeater test.

[Vanshilar]

I've updated the formula somewhat. What's been updated is that rather than trying to pigeon-hole the coefficient for how much each percentage of alacrity modifier increases the overall swing speed into 1* for THF and 1.2* for TWF, I changed them into whatever the linear fit deemed to be the best-fit values based on the data. It also turns out that, as MrCow said, THF are split into fast and slow types. The fast type gets a slightly bigger benefit from alacrity modifiers, while the slow type gets slightly less. Overall, the difference is somewhat less than 2% with 45% alacrity modifiers (i.e. with the haste spell and a haste boost 4), so it's small, but observable. I haven't tested falchions nor mauls yet so unsure about them. Also, I haven't tested the epic SoS yet to see if unique weapons (or at least, the eSoS) have the same swing speed as other weapons of the same type.

The big thing is probably that Rogue Acrobat II only provide a 5% bonus over Rogue Acrobat I, rather than the commonly recognized value of 10%. So acrobats should consider this when planning out their builds. Of course, acrobat + quarterstaff builds, if going to the second tier instead of the first, also gets the opportunist feat which stacks nicely with this.

Are you planning on calculating Twitch speeds for us THFs to consider?

I'll probably do it over Christmas break, once I'm done with finals.

Do you know of or plan to do a similar attack rate analysis for the ranged attacks, especially with and without manyshot?

Admittedly ranged is somewhat farther down the line in my list of priorities. The order that I'll be testing and posting results will likely be something like unarmed (monk) => twitch THF => BAB 16 testing of the above => ranged. Given how long it takes for me to go through the results though (mostly because I don't have that much time nowadays), no idea when I'll do ranged. My understanding though is that manyshot does not affect your rate of fire, although I haven't tested it. Depending on what people prefer I can look at twitch THF ahead of unarmed (monk) instead, but I felt it might be better to get all the major DPS styles out first before focusing on one type of a style (and no, I'm not considering ranged to be a major style of DPS ).

[karl_k0ch]

Thanks for the update. I totally understand that Ranged is rather low on your list. Also, as I realised later, the thread from the ranger forums which I linked some posts above tries to cover the question of ranged shots per minute. Hopefully, the data is being presented in a similarly nice way as here. So don't feel bad for not doing ranged right now.

MrCow puts Qstaff in the Slow THF class, whereas you put it into the fast one. Why's that?